In Terms Of Displayingã¢â‚¬â€¹ Data, How Is Aã¢â‚¬â€¹ Stem-and-leaf Plot Similar To A Dotã¢â‚¬â€¹ Plot?

Stem and foliage plots

Archived Content

Information identified as archived is provided for reference, inquiry or recordkeeping purposes. Information technology is not subject to the Government of Canada Web Standards and has not been contradistinct or updated since it was archived. Please contact us to asking a format other than those available.

Elements of a expert stem and leaf plot
Tips on how to draw a stalk and foliage plot
- Case 1 – Making a stem and foliage plot
The chief advantage of a stem and leaf plot
- Example 2 – Making a stem and leaf plot
- Case iii – Making an ordered stem and leaf plot
Splitting the stems
- Case 4 – Splitting the stems
- Example 5 – Splitting stems using decimal values
Outliers
Features of distributions
Using stem and leaf plots as graphs
- Instance half dozen – Using stem and leaf plots as graph

A stem and leaf plot, or stem plot, is a technique used to allocate either discrete or continuous variables. A stem and foliage plot is used to organize data as they are collected.

A stem and leaf plot looks something like a bar graph. Each number in the information is broken down into a stem and a leaf, thus the name. The stem of the number includes all only the last digit. The leaf of the number will ever be a single digit.

Elements of a skillful stem and leaf plot

A good stem and leaf plot

shows the offset digits of the number (thousands, hundreds or tens) equally the stem and shows the last digit (ones) as the leafage.
usually uses whole numbers. Anything that has a decimal point is rounded to the nearest whole number. For example, test results, speeds, heights, weights, etc.
looks like a bar graph when it is turned on its side.
shows how the data are spread—that is, highest number, everyman number, most common number and outliers (a number that lies outside the master grouping of numbers).

Meridian of Page

Tips on how to draw a stem and leafage plot

Once you have decided that a stem and leaf plot is the all-time mode to show your data, draw information technology equally follows:

On the left mitt side of the page, write downwards the thousands, hundreds or tens (all digits only the last i). These volition be your stems.
Draw a line to the right of these stems.
On the other side of the line, write down the ones (the terminal digit of a number). These will be your leaves.

For case, if the observed value is 25, then the stalk is 2 and the foliage is the 5. If the observed value is 369, then the stem is 36 and the leaf is 9. Where observations are accurate to one or more than decimal places, such every bit 23.7, the stem is 23 and the leafage is vii. If the range of values is too smashing, the number 23.7 tin be rounded up to 24 to limit the number of stems.

In stalk and leaf plots, tally marks are not required because the bodily information are used.

Not quite getting information technology? Try some exercises.

Instance ane – Making a stem and leaf plot

Each morning, a teacher quizzed his class with xx geography questions. The class marked them together and everyone kept a record of their personal scores. Every bit the year passed, each student tried to improve his or her quiz marks. Every mean solar day, Elliot recorded his quiz marks on a stalk and leafage plot. This is what his marks looked like plotted out:

Tabular array one. Elliot's scores on the bones facts quiz last year
Stalk	Leaf
0	3 6 5
1	0 1 4 three 5 6 5 6 8 9 seven nine
2	0 0 0 0

Analyse Elliot'due south stem and leaf plot. What is his most common score on the geography quizzes? What is his highest score? His lowest score? Rotate the stalk and leaf plot onto its side so that it looks like a bar graph. Are about of Elliot's scores in the 10s, 20s or under x? Information technology is difficult to know from the plot whether Elliot has improved or not considering nosotros practise non know the club of those scores.

Try making your own stem and leaf plot. Use the marks from something like all of your exam results final year or the points your sports squad accumulated this season.

Height of Page

The chief reward of a stem and leaf plot

The master advantage of a stem and leaf plot is that the data are grouped and all the original information are shown, too. In Example iii on battery life in the Frequency distribution tables section, the table shows that two observations occurred in the interval from 360 to 369 minutes. However, the tabular array does not tell yous what those bodily observations are. A stem and leaf plot would bear witness that information. Without a stem and leaf plot, the two values (363 and 369) can simply be found by searching through all the original data—a tedious task when yous have lots of information!

When looking at a information fix, each observation may exist considered equally consisting of 2 parts—a stalk and a foliage. To brand a stem and leaf plot, each observed value must first be separated into its two parts:

The stalk is the offset digit or digits;
The foliage is the final digit of a value;
Each stem can consist of any number of digits; but
Each leaf tin can have only a single digit.

Top of Page

Example 2 – Making a stem and leaf plot

A teacher asked 10 of her students how many books they had read in the terminal 12 months. Their answers were as follows:

12, 23, 19, half-dozen, ten, 7, 15, 25, 21, 12

Prepare a stem and leaf plot for these information.

Tip: The number 6 can be written every bit 06, which means that it has a stem of 0 and a leaf of vi.

The stalk and foliage plot should look like this:

Table 2. Books read in a twelvemonth by 10 students
Stem	Foliage
0	half dozen seven
i	2 9 0 v ii
ii	three 5 1

In Table 2:

stalk 0 represents the form interval 0 to ix;
stem one represents the grade interval 10 to 19; and
stem 2 represents the course interval 20 to 29.

Usually, a stem and leaf plot is ordered, which simply means that the leaves are arranged in ascending social club from left to right. Also, in that location is no need to carve up the leaves (digits) with punctuation marks (commas or periods) since each leafage is always a single digit.

Using the data from Table 2, nosotros made the ordered stem and leafage plot shown below:

Tabular array three. Books read in a yr by 10 students
Stem	Leaf
0	6 7
1	0 2 2 5 9
2	i iii 5

Summit of Page

Example three – Making an ordered stem and leaf plot

Fifteen people were asked how oft they drove to work over ten working days. The number of times each person collection was every bit follows:

5, vii, 9, 9, 3, 5, 1, 0, 0, 4, 3, 7, 2, ix, 8

Make an ordered stalk and leaf plot for this table.

It should be drawn equally follows:

Tabular array iv. Number of drives to work in 10 days
Stem	Leaf
0	0 0 1 ii iii iii 4 5 v seven 7 viii nine 9 ix

Splitting the stems

The organization of this stem and foliage plot does non give much data about the information. With only ane stem, the leaves are overcrowded. If the leaves become too crowded, then it might be useful to separate each stalk into two or more components. Thus, an interval 0–9 can be split into two intervals of 0–iv and 5–nine. Similarly, a 0–9 stem could be split into five intervals: 0–ane, ii–3, 4–five, half dozen–7 and viii–nine.

The stalk and foliage plot should then look like this:

Table v. Number of drives to work in 10 days
Stem	Leaf
0⁽⁰⁾	0 0 1 2 3 3 iv
0⁽⁵⁾	v 5 7 vii 8 9 9 9

Note: The stem 0⁽⁰⁾ means all the data inside the interval 0–four. The stem 0⁽⁵⁾ means all the information within the interval 5–9.

Top of Page

Instance 4 – Splitting the stems

Britney is a swimmer training for a competition. The number of 50-metre laps she swam each day for 30 days are as follows:

22, 21, 24, 19, 27, 28, 24, 25, 29, 28, 26, 31, 28, 27, 22, 39, 20, 10, 26, 24, 27, 28, 26, 28, 18, 32, 29, 25, 31, 27

Prepare an ordered stem and leaf plot. Make a cursory comment on what it shows.
Redraw the stem and leaf plot by splitting the stems into five-unit intervals. Make a brief annotate on what the new plot shows.

Answers

The observations range in value from 10 to 39, so the stem and leaf plot should have stems of 1, 2 and 3. The ordered stalk and foliage plot is shown below:

Table vi. Laps swum by Britney in thirty days
Stem	Leaf
1	0 8 9
2	0 i 2 ii iv four 4 5 5 half-dozen 6 6 vii seven 7 vii 8 eight 8 viii 8 ix 9
3	ane i 2 9

The stalk and leafage plot shows that Britney usually swims between 20 and 29 laps in training each day.

Splitting the stems into five-unit intervals gives the following stem and foliage plot:

Table 7. Laps swum by Britney in 30 days
Stem	Leaf
1⁽⁰⁾	0
1⁽⁵⁾	eight 9
2⁽⁰⁾	0 1 2 ii 4 4 four
2^(five)	five 5 6 6 6 7 7 7 seven 8 8 8 8 8 9 9
3⁽⁰⁾	1 1 2
3^(v)	nine

Note: The stem 1⁽⁰⁾ ways all data between x and 14, 1^(v) means all data between xv and xix, and so on.

The revised stem and leaf plot shows that Britney usually swims betwixt 25 and 29 laps in training each day. The values 1⁽⁰⁾ 0 = x and 3⁽⁵⁾ 9 = 39 could exist considered outliers—a concept that will be described in the adjacent department.

Top of Page

Example 5 – Splitting stems using decimal values

The weights (to the nearest tenth of a kilogram) of xxx students were measured and recorded as follows:

59.ii, 61.5, 62.3, 61.four, sixty.9, 59.8, threescore.five, 59.0, 61.ane, 60.7, 61.half dozen, 56.iii, 61.ix, 65.7, 60.4, 58.ix, 59.0, 61.2, 62.1, 61.4, 58.4, threescore.8, threescore.2, 62.seven, 60.0, 59.3, 61.9, 61.vii, 58.4, 62.2

Set up an ordered stalk and leaf plot for the data. Briefly annotate on what the analysis shows.

Answer

In this example, the stems volition be the whole number values and the leaves volition be the decimal values. The data range from 56.3 to 65.7, so the stems should start at 56 and finish at 65.

Table 8. Weights of 30 students
Stem	Leaf
56	3
57
58	4 iv ix
59	0 0 2 3 viii
60	0 2 4 5 vii viii ix
61	ane 2 4 4 5 six seven ix 9
62	one 2 3 seven
63
64
65	7

In this example, it was not necessary to split stems because the leaves are non crowded on also few stems; nor was information technology necessary to round the values, since the range of values is not large. This stem and leafage plot reveals that the group with the highest number of observations recorded is the 61.0 to 61.9 group.

Top of Page

Outliers

An outlier is an extreme value of the data. It is an observation value that is significantly different from the rest of the data. There may be more than one outlier in a fix of data.

Sometimes, outliers are significant pieces of information and should not be ignored. Other times, they occur because of an fault or misinformation and should be ignored.

In the previous example, 56.3 and 65.7 could be considered outliers, since these 2 values are quite unlike from the other values.

Past ignoring these two outliers, the previous example'southward stem and leaf plot could be redrawn as below:

Table 9. Weights of 30 students except for outliers
Stem	Leafage
58	four four 9
59	0 0 2 3 viii
lx	0 2 4 5 seven eight 9
61	1 2 4 four 5 6 7 9 9
62	1 2 iii 7

When using a stalk and leafage plot, spotting an outlier is ofttimes a thing of judgment. This is because, except when using box plots (explained in the section on box and whisker plots), in that location is no strict rule on how far removed a value must be from the residual of a data gear up to qualify every bit an outlier.

Top of Page

Features of distributions

When yous assess the overall pattern of any distribution (which is the pattern formed by all values of a item variable), look for these features:

number of peaks
general shape (skewed or symmetric)
heart
spread

Number of peaks

Line graphs are useful because they readily reveal some characteristic of the data. (See the section on line graphs for details on this type of graph.)

The first characteristic that can be readily seen from a line graph is the number of high points or peaks the distribution has.

While virtually distributions that occur in statistical data accept merely one main peak (unimodal), other distributions may have two peaks (bimodal) or more than two peaks (multimodal).

Examples of unimodal, bimodal and multimodal line graphs are shown below:

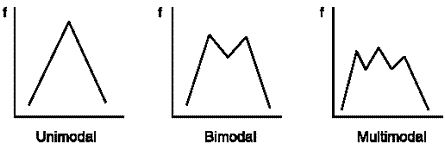
Examples of unimodal, bimodal and multimodal line graphs.

General shape

The second main feature of a distribution is the extent to which it is symmetric.

A perfectly symmetric bend is one in which both sides of the distribution would exactly match the other if the figure were folded over its central signal. An instance is shown beneath:

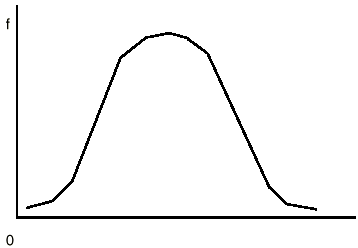
Example of a perfectly symmetric curve.

A symmetric, unimodal, bell-shaped distribution—a relatively common occurrence—is called a normal distribution.

If the distribution is lop-sided, information technology is said to be skewed.

A distribution is said to exist skewed to the right, or positively skewed, when most of the data are concentrated on the left of the distribution. Distributions with positive skews are more mutual than distributions with negative skews.

Income provides one instance of a positively skewed distribution. Most people make under $forty,000 a year, but some make quite a bit more, with a smaller number making many millions of dollars a year. Therefore, the positive (correct) tail on the line graph for income extends out quite a long way, whereas the negative (left) skew tail stops at nothing. The right tail clearly extends farther from the distribution's centre than the left tail, every bit shown below:

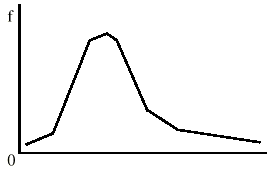
Example of a positively skewed distribution.

A distribution is said to be skewed to the left, or negatively skewed, if most of the data are full-bodied on the right of the distribution. The left tail clearly extends farther from the distribution's centre than the right tail, every bit shown below:

Example of a negatively skewed distribution.

Centre and spread

Locating the centre (median) of a distribution tin be washed by counting one-half the observations up from the smallest. Obviously, this method is impracticable for very large sets of data. A stem and leafage plot makes this easy, even so, because the data are arranged in ascending order. The mean is another mensurate of central trend. (See the chapter on central tendency for more detail.)

The corporeality of distribution spread and any large deviations from the general pattern (outliers) can be chop-chop spotted on a graph.

Using stalk and leaf plots every bit graphs

A stalk and leaf plot is a simple kind of graph that is made out of the numbers themselves. Information technology is a means of displaying the master features of a distribution. If a stalk and leaf plot is turned on its side, it will resemble a bar graph or histogram and provide similar visual information.

Acme of Page

Case 6 – Using stem and foliage plots equally graph

The results of 41 students' math tests (with a best possible score of 70) are recorded below:

31, 49, 19, 62, 50, 24, 45, 23, 51, 32, 48, 55, 60, 40, 35, 54, 26, 57, 37, 43, 65, 50, 55, eighteen, 53, 41, fifty, 34, 67, 56, 44, 4, 54, 57, 39, 52, 45, 35, 51, 63, 42

Is the variable discrete or continuous? Explain.
Ready an ordered stem and leaf plot for the information and briefly depict what it shows.
Are at that place any outliers? If so, which scores?
Look at the stem and foliage plot from the side. Describe the distribution's primary features such as:
1. number of peaks
2. symmetry
3. value at the middle of the distribution

Answers

A test score is a discrete variable. For case, information technology is not possible to take a test score of 35.74542341....

The lowest value is 4 and the highest is 67. Therefore, the stem and leaf plot that covers this range of values looks similar this:

Tabular array 10. Math scores of 41 students
Stem	Leaf
0	4
i	viii 9
2	three 4 6
iii	one 2 4 five v seven 9
4	0 1 two iii 4 v 5 8 nine
5	0 0 0 one ane 2 3 4 4 five 5 half dozen 7 seven
6	0 two 3 five 7

Note: The notation 2|4 represents stem 2 and leaf 4.

The stem and leaf plot reveals that most students scored in the interval betwixt 50 and 59. The large number of students who obtained high results could mean that the test was too like shooting fish in a barrel, that most students knew the cloth well, or a combination of both.

The result of 4 could be an outlier, since at that place is a big gap betwixt this and the adjacent result, 18.
If the stem and foliage plot is turned on its side, it will look similar the following:

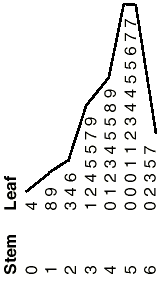
The distribution has a single peak within the 50–59 interval.

Although there are only 41 observations, the distribution shows that virtually data are clustered at the correct. The left tail extends farther from the data middle than the right tail. Therefore, the distribution is skewed to the left or negatively skewed.

Since at that place are 41 observations, the distribution centre (the median value) will occur at the 21st ascertainment. Counting 21 observations up from the smallest, the centre is 48. (Note that the same value would take been obtained if 21 observations were counted down from the highest observation.)